Why do I believe that my career will involve creating a job and / or an industry?
Well even now with the business I’m starting, it’s getting into a very new, prime industry. Not too many people have programs for Life OS, but even fewer, if any, that do that do 1x1 instead of in a group cohort setting.
Is it scalable?
It is if the price is high enough. Well that answers more of the question of if it’s financially viable, sustainable, and growable.
Now scalability - does it need to be a different model than the cohort model to make it customizable? Because that personalization is sacrificed to get a larger volume of change. Which is also noble, but where is that line between quantity & quality? Where is that balance?
I want more people to be coaches who teach and implement this. And take it to even new heights. A question I’ve asked before and one I’ll ask again here is “Would the world be a better place if more of my business existed?” If there were more Life OS’s out there, then I definitely shouldn’t be limiting the growth of this industry based on a monetary goal that I have.
So how can I structure it so that there are more coaches teaching some Life OS and some Organizational OS?
The quality of someone’s Life OS is more important to me because if they are more bought into their own Life OS, then they’ll naturally exude that energy to share their ways of their Life OS.
Let’s say I have a group cohort of 20 people, I won’t be able to spend 1x1 time with them as I could if I did 4 1x1 clients, for example.
Let’s say 75% of my 1x1 clients are eager enough to share with others also in a 1x1 setting. Let’s say 10% of people from the cohort are in that same mindset. Then it’s 2 out of 20.
Well these are arbitrary numbers. I just made them work to fit my case.
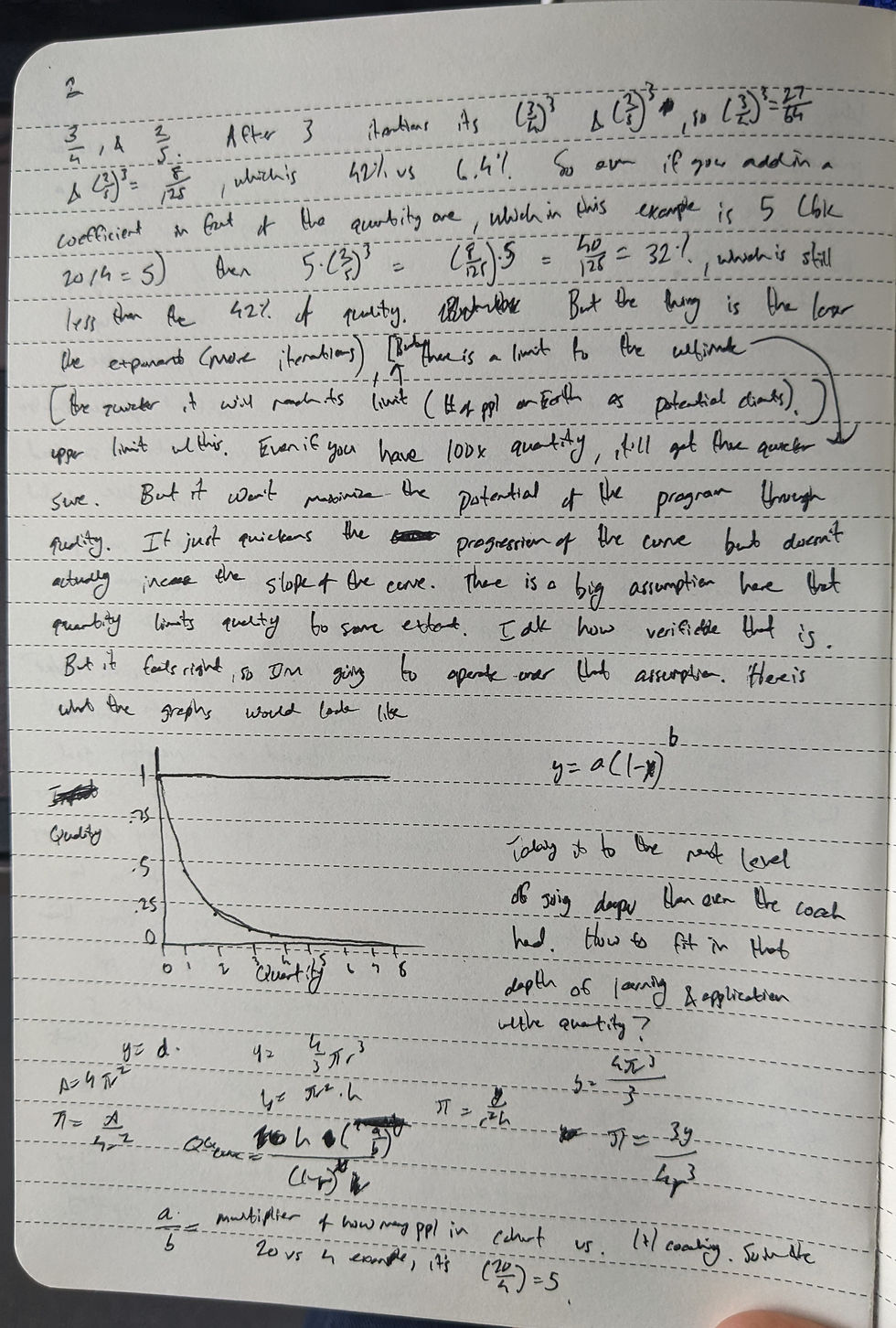
So let’s say it’s 75% and 40% for 1x1 and group cohort, respectively. 3/4 and 2/5. After 3 iterations, it’s (3/4)^3 and (2/5)^3, which equal 27/64 and 8/125, respectively. Those are 42% and 6.4%. So even if you add in a coefficient in front of the quantity one, which in this example is 5 (because 20/4 = 5), then 5*(2/5)^3 = (8/125)*5 = 40/125 = 32%, which is still less than the 42% of quality.
But the thing is the larger the exponent (more iterations), the quicker it will reach its limit (# of people on Earth as potential clients). But there is a limit to the ultimate upper limit with this. Even if you have 100x quantity, it’ll get there quicker sure. But it won’t maximize the potential of the program through quality. It just quickens the progression of the curve but doesn’t actually increase the slope of the curve.
There is a big assumption here that quantity limits quality to some extent. Idk how verifiable that is. But it feels right, so I’m going to operate under that assumption. Here is what the graphs would look like.
[see pics for 15 min of graphing & attempting to quantify]
(Taking it to the next level of going deeper than even the coach had. How to fit in that depth of learning and application with the quantity?)
QQ curve = h*(a/b) / (1-r)^x
a/b = multiplier of how many people in cohort vs 1x1 coaching. So in the 20 vs 4 example, it’s (20/4) = 5. (1-r), where r is how much of the knowledge of the coach is transferred effectively to the student / client.
So if 70% of the material is transferred, then it’s 1-.3 = .7. Actually, let’s just make it r instead of 1-r, not to complicate things. But 0 ≤ r ≤ 1. And where h = coefficient of the application of the learnings for the client. For r, there’s an upper bound of 1 but h theoretically doesn’t have a limit because it has infinite potential to be applied in any way.
Let’s rename the variables so they’re more indicative of what they signify.
y = a*(n/m) / k^x.
Where,
y = Quality-Quantity curve
a = application of the knowledge (group & individuals)
n/m = multiplier of the # of people in quantity based course vs quality based course
k = knowledge of coach that’s transferred, where 0 ≤ k ≤ 1
x = # of iterations.
Ok does this make sense? Let’s plug in numbers I guess and see what happens.
a = 2, (n/m) = 4, k = .8, x=2.
Actually, the k^x term needs to be in the numerator because it’s going to be always less than or equal to 1.
So 8(.64) = 5.12
Hmm, should ‘a’ be outside or inside the parentheses? Like y = am(k^x) or y = m*(ak)^x.
Plugging in numbers to the latter one with ‘ak’ as one term, then quantity and quality based courses could equal, respectively:
y = 4(1.25*.75)^x = 4(.9375)^x
y = (1/4)(1.25*.95)^x. = 1/4*(1.1875)^x.
Are these accurate / directional assumptions of a and k?
I actually think the network effect of the group cohort and the customizability of the 1x1 coaching offset each other so hence both being 1.25. With 1 as where I am baselining as if the coach were to just give templates to the client, then that’s a 1, if not a bit lower because the client may not know everything that’s in that template.
But the difference then comes in k. Which is the knowledge of the coach that’s transferred. So in a group cohort, a coach might have a 60 minute call each week generally along with a 30 minute video and let’s say 2-5 questions answered per client across the platforms, including on a community members area.
1x1 coaching may have those same 60 minute call and 30 minute video but in the text chat and call, the coach can answer let’s say 5-10 questions because of that dedicated coach-client time. That means it’s at least 26% difference (.75 vs .95) in 1x1 vs cohort. At least that was the assumption. And I think those sample numbers are conservative in favor of 1x1 setting.
With those sample numbers, after 2 iterations (x=2), it’s y = 3.51625 & y = .35.
x = 3: y = 3.29, y = .41
x = 10: y = 2.1, y = 1.4
x = 15: y = 1.5, y = 3.3
But the x’s are not created equal here. When x = 15 for the cohort based course, that could be 20 * 15 = 300 if 20 people in each cohort. But x = 15 for 1x1 coaching is 15 * 4 = 60. Which means that x will have to equal to 75 (300/4) when it’s also reached 300. And with x = 75, then y = (1/4)*(1.1875)^75 = 98,960.
So essentially, all this to say that quality scales and quantity necessarily doesn’t.
This equation probably only applies to courses and programs with the 1x1 vs cohort based courses but I’m sure the principle can be applied generally, that quantity scales, even though it sounds oxymoronic.
LOL I never answered the original question. But basically since I’m always creating something, at least theoretically, conceptually, systemically, and now recently quantifiably with semantics as well, I think this is the only natural order of progression.
I think one of those things will be a subfield Semantics called Quantifiable or Mathematical Semantics.
We’ll see what others there are.





Comments